El andarín borracho regresa a casa…
Peeero, su pájaro se pierde para siempre…
Imaginemos un borracho caminando aleatoriamente por una ciudad cuyas calles forman una malla cuadrada. En cada cruce, el borracho elige una de las cuatro posibles direcciones que dan a ese cruce (incluyendo aquella por la que ha venido) con la misma probabilidad. Formalmente, esto sería lo que llamamos un paseo aleatorio en el plano.
El problema de saber si el señor borracho podrá llegar, eventualmente, desde el bar a su casa, caminando al azar, tiene una respuesta afirmativa. Pero si realizamos un problema similar con 3 o más dimensiones, no sucede así. En otros términos, un pájaro despistado podría vagar al azar por el cielo por siempre sin encontrar nunca su nido.

Aunque parezca alucinante, en dos dimensiones siempre volverás a lugar donde comiences, es decir, tu punto de partida, haciendo movimientos… Sin embargo, lo mismo no se puede decir de tres dimensiones, todo cambia sólo porque usted puede subir y bajar… Realmente esa situación es muy extraña.
Eso de vagar sin rumbo, a la buena ventura, como lo haría un trotamundos empedernido son ejemplos de conductas imprevisibles, como lo son por ejemplo, las del legendario Caballero de la Mancha, las cuales provocaron la admiración de todos sus lectores al ver la valentía con que enfrentaba los inesperados lances que provocan tan azarosas sendas.
… y con esto se quietó y prosiguió su camino,
sin llevar otro que aquel que su caballo quería,
creyendo que en aquello consistía la fuerza de las aventuras.
Don Quijote, Primera parte, Cap. II

Los matemáticos tienen la pertinaz costumbre de analizar todo lo analizable, y las caminatas sin rumbo no iban a ser excepción. Matemáticamente hablando, son tan ricas en aventuras como las andanzas del Ingenioso Hidalgo.
En efecto, los paseos aleatorios son una de las principales ramas de la “Teoría de Cadenas de Markov”, que a su vez son uno de los más candentes temas de la moderna teoría de probabilidades, en razón de su creciente aplicación científica. Así, las caminatas aleatorias pueden utilizarse para modelar fenómenos que ocurren en el mundo real, desde movimientos de moléculas en un gas hasta el comportamiento de un apostador que pasa un día en el casino. En efecto, los resultados del estudio de las caminatas aleatorias han sido aplicados a muchos campos como la computación, la física, la química, la ecología, la biología, la psicología o la economía.
En su forma más general, las caminatas aleatorias son cualquier proceso aleatorio donde la posición de una partícula en cierto instante depende solo de su posición en algún instante previo y alguna variable aleatoria que determina su subsecuente dirección, así como la longitud de su paso.
La teoría relacionada con caminatas aleatorias se desarrolla en el marco general de la teoría de los “Procesos Estocásticos”, más exactamente con las mencionadas cadenas de Márkov. En efecto, a menudo, los caminos aleatorios se suponen que son cadenas de Márkov.
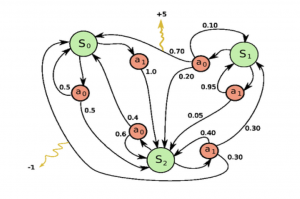
Una cadena de Márkov (así llamada en honor del matemático ruso A. A. Márkov, el primero en estudiarlas) es un sistema de «estados» discretos más un sistema de probabilidades de transición de unos estados a otros, probabilidades que han de ser independientes de la Historia, es decir, de la evolución del sistema en el pasado. Entre los ejemplos más sencillos de tales cadenas tenemos la caminata aleatoria a lo largo del segmento rectilíneo compuesta de pasos discretos a lo largo de una recta.
Un problema clásico dentro de los paseos aleatorios unidimensionales es el conocido como la “Ruina del Apostador”, referido a un jugador “A”, con una cantidad finita de dinero, que juega a un juego no sesgado contra una banca “B” que tiene infinito dinero… Ambos van apostando sistemáticamente, por ejemplo a «cara o cruz».
Cuando sale cara, B le paga un dólar a A; por cada cruz, A le da un dólar a B. El juego termina tan pronto como uno de los jugadores queda «arruinado», es decir, se queda sin dinero.
Lamentablemente “A” siempre terminará perdiendo. La cantidad de dinero del jugador efectuará un paseo aleatorio según vaya ganando o perdiendo, y siempre, en algún momento, alcanzará el 0 y el juego terminará. Es fácil comprender la correspondencia entre el desarrollo de este juego y las andanzas del caminante. Ambas interpretaciones dan iguales respuestas a todas las cuestiones probabilísticas referentes a ellas.
En efecto, la probabilidad de victoria de cada jugador está dada por su capital inicial dividido por el total de dólares que poseen entre ambos y la suma de ambas probabilidades tiene que ser 1 (probabilidad de la certeza, o del «suceso seguro»).
La interpretación intuitiva de este hecho es que si la partida, o el paseo, durase lo suficiente, es seguro que tendrá fin, es decir, estamos diciendo que si A se enfrenta a un contrincante con capital infinito, es seguro que A terminará arruinado. Malas noticias, pues, para los jugadores empedernidos. Aun cuando todas sus apuestas fuesen equitativas, como están enfrentándose a un «oponente» (todos los demás jugadores del mundo) cuyo capital es virtualmente ilimitado, tienen garantizada la ruina.
Los paseos aleatorios también lo podemos hacer en el plano y en el espacio.
En el plano a cada paso el caminante, borracho o no, va de un vértice de un retículo cuadriculado a otro vértice contiguo, por ello, en el plano, se llama caminata aleatoria, a una cadena que describe el movimiento aleatorio a lo largo de los vértices de un retículo cuadriculado. Es decir, si el andarín está en un vértice en un momento dado, entonces estará en un vértice vecino en el siguiente momento, donde el vértice vecino será escogido aleatoriamente.
Ahora bien, en el caso que pueda vagabundear sin restricciones en un retículo infinito la situación se complica y en este caso se han demostrado algunos teoremas que no sólo son profundos sino también paradójicos.
Si la duración del paseo es suficientemente larga, es seguro que el paseante visitará todo vértice del retículo, incluido el punto de partida. Por otra parte, si el paseo prosigue un tiempo arbitrariamente largo, la proporción de veces que el paseante visita un vértice determinado tiende a cero. Estas nociones sirven muy bien para presentar la diferencia radical entre los conceptos de posibilidad lógica y posibilidad práctica.
Desde el punto de vista lógico, existe la posibilidad lógica de que el caminante pueda estar paseándose eternamente sin pasar por un determinado vértice. Para el estadístico, empero, la probabilidad práctica, la plausibilidad, es nula, a pesar de que el número esperado de pasos para alcanzar un vértice prefijado cualquiera sea infinito.
Así lo expresa Kemeny: si estamos parados en uno de los cruces del retículo infinito, mientras un amigo nuestro, partiendo de otro cruce cualquiera, se dedica a vagar sin rumbo por la red de calles, podríamos tener la certeza práctica de acabar reuniéndonos con él, siempre y cuando estemos dispuestos a esperar tanto como haga falta.
Recibimos sorpresas mayores al estudiar generalizaciones a espacios de dimensión mayor. En un retículo tridimensional (cúbico o no) finito, es prácticamente seguro que un paseante que vaya recorriéndolo al azar llegará a cualquier intersección en un tiempo finito. En cambio, cuando el retículo sea infinito no sucederá así.
George Polya demostró, allá por 1921, que la probabilidad de que en una red tridimensional la caminata aleatoria pase por un vértice prefijado es menor que 1, aunque el paseo se prolongue toda la eternidad.
Con un poco de mayor formalmente podríamos escribir que:
Sea p(d) la probabilidad de que un paseo aleatorio sobre un retículo de dimensión d regrese a su punto de partida. Se verifica que:
p(1) = p(2) = 1 y p(d) < 1 si d > 2.
Dicho de otro modo, los paseos aleatorios en dimensiones 1 y 2 son recurrentes y en dimensiones mayores que 2 son transitorios.
En 1940, W. H. McCrea y F. J. H. Whipple demostraron que la probabilidad de que el pájaro retorne al origen de su caminata es de sólo: p(3) = 0,34053732955099914282627318443… Es decir, tiene menos del 35% de probabilidad de volver a su punto de partida, aunque el paseo se prolongue indefinidamente. Bueno, por cierto esto sería así si el cielo fuera infinito. Puesto que nuestra atmósfera tiene un volumen finito, creo que el pájaro ¡bravo! siempre volverá a casa…

Un saludo de un lector que, caminando aleatoriamente por internet, ha ido a caer aquí, y que comparte su afición aquí expuesta.
Entretenida lectura, felicitaciones!
Super interesante, es digno el material de vincularse a las clases de series de tiempo.
Excelente artículo, muy interesante!
Buena información y didactica
Excelente lectura, muy interesante, la recomendaré a mis alumnos de posgrado en la clase de procesos estocásticos.