Al igual que en Física nos encontramos con agujeros negros de los que nada puede escapar de ellos, ni siquiera la luz, también en Matemáticas se da esta curiosidad científica.
En efecto, hay secuencias de operaciones que siempre nos llevan a un «Black hole», que atrae al resto de números, independientemente del número del cual partamos.
La Conjetura de Collatz es un caso de ello. Fue enunciada por el matemático Lothar Collatz en 1937, Desde entonces, una serie de matemáticos han intentado probar esta conjetura, pero se ha quedado sin probarla, y a la fecha no se ha resuelto.
Veamos cómo opera…
Sea la siguiente operación, aplicable a cualquier número entero positivo:
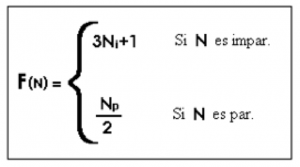
Si el número es impar, se multiplica por 3 y se suma 1.
Si el número es par, se divide entre 2.
Es decir, tome cualquier número entero positivo, o «n». Si n es par, divídalo por 2 para obtener n / 2. Si n es impar, multiplíquelo por 3 y añada 1 para obtener 3n + 1. Repita el proceso indefinidamente.
La conjetura es que no importa con qué número comienzas, siempre llegarás a 1 (y por tanto al ciclo 4, 2, 1). Veamos un par de ejemplos:
Empieza con 21. Es impar, así que multiplico por 3 (21X3 es 63) y enseguida le sumo 1, para obtener como resultado 64. Ahora 64 es par, por lo que lo divido entre 2 y se obtiene 32, de nuevo nos resulta un número par, y por ello repito la división entre dos para obtener 16, 8, 4, 2, 1.
Empezando en n = 11, la sucesión tarda un poco más en alcanzar finalmente el 1, se desarrollaría de la forma siguiente:
11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

Nadie ha encontrado un número que no sigue esta regla… Aún no se ha demostrado la veracidad, ni falsedad, del resultado, aunque este año (2017) se comprobó la conjetura para todas las secuencias de números menores que 87 × 2 60. Esta es una fuerte evidencia intuitiva a favor de la veracidad del resultado, a pesar de no aportar nada, formalmente hablando, en el terreno de las matemáticas. Es más, a veces los únicos contraejemplos de una conjetura se encuentran cuando se usan números muy, muy, grandes.
Lo cierto es que de este «potente» problema podemos pasar a una actividad de escolar… Es que estos tipos de problemas pueden inspirar actividades de clase muy ricas tanto para Primaria, como para Secundaria.
Veamos un ejemplo para alumnos de tercer grado…
Para facilitarlo al comienzo, lo modificaremos un poco, acotándolo hasta 40 y eliminando la multiplicación por tres…Así:
«Elegir un número entre 0 y 40. Si es par, se divide por 2. Si es impar, le sumamos 1 y repetimos este proceso hasta llegar a 1.»
¿Con qué número consigo hacer la secuencia más larga?
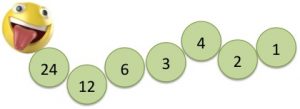
Para explicar las instrucciones se puede partir de un gusano en el que el primer número era el 24 planteando que el gusano «se acabaría» cuando llegaran al número 1.
La primera discusión ya fue como calcular la mitad de 24, que no es elemental para un tercer grado, poco a poco se llegará a completar el gusano y a contar que tiene 7 anillas:
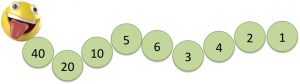
Una vez familiarizados con el cálculo de mitades, en otra sesión se puede plantear encontrar un gusano más largo, con la condición de que el primer número no podía ser mayor de 40, se podrá dibujar en la pizarra un gusano que tendrá 9 anillas:
Ahora se podría preguntar ¿realmente ese sería el más largo?… ¿y si no ponemos el límite hasta 40? En fin, una muy buena actividad que seguro generará muy buenas preguntas al retar a los estudiantes, claro, se necesita una maestra que quiera hacer maravillosa a la matemáticas.
Finalmente, acá les dejo una bonita visualización de la Conjetura

Quisiera compartir o discutir con ustred esta publicacion mia a ver qué le parece
La conjetura dice que siempre alcanzaremos el 1, para cualquier número con el que comencemos.
Las secuencias de Collatz para n variando entre 2 y 26 son:
2 1
3 10 5 16 8 4 2 1
4 2 1
5 16 8 4 2 1
6 3 10 5 16 8 4 2 1
7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
8 4 2 1
9 28 14 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
10 5 16 8 4 2 1
11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
12 6 3 10 5 16 8 4 2 1
13 40 20 10 5 16 8 4 2 1
14 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
15 46 23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1
16 8 4 2 1
17 52 26 13 40 20 10 5 16 8 4 2 1
18 9 28 14 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
19 58 29 88 44 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
20 10 5 16 8 4 2 1
21 64 32 16 8 4 2 1
22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1
24 12 6 3 10 5 16 8 4 2 1
25 76 38 19 58 29 88 44 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
26 13 40 20 10 5 16 8 4 2 1
Ahora tome una cuelquiera de las secuencias obtenidas.
Yo voy a coger la del 25.
Cuente el número de pares (16) y haga n= 2^16.
Después tome 16 y réstele el número de pares hasta el primer impar empezando por el final (16-4= 12).
Réstele a n la potencia 3^0*2^12 = 2^12
Ahora réstele a 12 el número de pares hasta el siguiente impar del anterior (12-3=9) y réstele a n la expresión 3^1*2^9.
Siga este proceso hasta el 25 multiplicando cada potencia de 2 obtenida según el proceso por la potencia de 3 siguiente en orden creciente (3^2, 3^3,…etc), obtendrá la expresión n=2^16-2^12-3*2^9-3^2*2^7-3^3*2^6-3^4*2^3-3^5*2^2-3^6
En este caso resultará n=54675.
Si ahora dividimos este número por la potencia de 3 con exponente el número de impares de la secuencia ( que son 7), obtendremos n=54675/3^7=25!!
Es casualidad?
No, escoja el número que escoja al hacer las operaciones indicadas obtendrá el primer número de la secuencia de Collatz.
Esto se traduce que, en general:
n= (2^a(1) – 2^a(2) – 3*2^a(3) – 3^2*2^a(4) – … – 3^(s-2)*2^a(s) – 3^(s-1)*2^a(s+1))/3^(s)
donde a(i) es una secuencia decreciente de s+1 enteros positivos con a(1)= número de pares de la secuencia de Collatz, s el número de impares de dicha secuencia y a(j) es a(j – 1) menos el número de pares que hay entre el impar del lugar j – 2 y el del lugar j -1 empezando por el final ( el que ocupa el lugar 0 siempre es el 1, final de toda secuancia de Collatz).