El cuerno de Gabriel (también llamado trompeta de Torricelli) es una figura geométrica que tiene la característica de poseer una superficie infinita pero un volumen finito.
El nombre se refiere a la tradición que identifica al Arcángel Gabriel como el ángel que toca el cuerno para anunciar el Día del Juicio, asociando lo divino, o infinito, con lo finito.
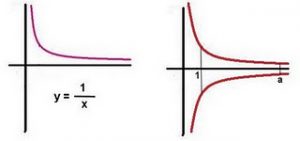
Matemáticamente es la superficie de revolución que se obtiene al girar, en tres dimensiones, alrededor del eje X (que es el eje de rotación), el gráfico de la función F(x)=1/x, (la generatriz) con dominio x ≥ 1.
Las propiedades de esta figura fueron estudiadas por el físico y matemático italiano Evangelista Torricelli, que fue estudiante de Galileo, hacia 1641 (anterior al Cálculo), que la bautizó como un sólido hiperbólico agudo.
Las propias palabras de Torricelli describen completamente su asombro al descubrir un sólido infinitamente largo con una superficie que calcula tener un área infinita, pero un volumen finito.
En el momento de su descubrimiento, fue considerado una paradoja, lo que llevó a Torricelli a probar varias pruebas alternativas. Esta paradoja aparente ha sido descrita de modo informal señalando que sería necesaria una cantidad infinita de pintura para cubrir la superficie exterior, mientras que sería posible rellenar toda la figura con una cantidad finita de pintura y así cubrir esa superficie.
Lo cierto es que Torricelli nació “un poco” demasiado pronto. El estudio del infinitesimal era demasiado nuevo. Recordemos que Newton nació el año en que Galileo había muerto (1642) y Leibniz era todavía cuatro años más joven.
Desafortunadamente, Torricelli no vivió para ver los métodos del cálculo completamente emerger para confirmar sus cálculos minuciosos basados en gran parte en el método de su amigo Cavalieri, hoy conocido como el “Principio de Cavalieri” de la «suma de las rebanadas planas» (Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, poseen entonces igual volumen).
Debo agregar que la aparente paradoja formó parte de una disputa sobre la naturaleza del infinito que implicaba a muchos de los pensadores clave de aquella época, incluyendo a Thomas Hobbes, John Wallis y el mencionado Galileo Galilei.
Es posible calcular tanto el volumen, como el área superficial del cuerno entre x = 1 y x = a, donde a > 1 y es tan grande como se desee.
El volumen del cuerno, entre x=1 y x=a se acercará más y más a pi conforme “a” crece. Matemáticamente se dice que el volumen tiende a pi «π» a medida que “a” tiende a infinito. Lo cual se expresa:
V = (1- 1/a) = π
Con respecto al área entre x=1 y x=a, se tiene que es:
A = 2π Ln a
Y como no existe una cota superior para el logaritmo neperiano de “a” conforme tienda a infinito, quiere decir que, en este límite, el cuerno de Gabriel tiene un área superficial infinita.
Ahhh, debo finalmente mencionar que el fenómeno inverso del cuerno de Gabriel, es decir, tener una superficie de revolución que tenga una superficie finita pero un volumen infinito, no puede ocurrir. En efecto:
Teorema:
Sea f: [1, ∞) → [0, ∞) una función continuamente diferenciable.
Escriba S para el sólido de revolución del gráfico y= f(x) sobre el eje X. Si el área superficial de S es finita, entonces también lo es su volumen. Puedes ver una demostración aquí
No me dirás que no es una bella curiosidad matemática la “paradoja” del Cuerno de Gabriel… Ahhh y la semana próxima nos vamos de fiesta… Nos vamos de Halloween… ¿Vale?