Newton y sus «Principios Matemáticos de la Filosofía Natural»… ¡Vaya nombre perfecto!

Primera Ley de Newton

Bajo esta óptica, veamos el principio de conservación de la velocidad, también llamado «Primera Ley de Newton» que se conoce también como «Principio de Inercia»:

Un móvil sobre el que no actúa fuerza alguna mantiene indefinidamente la misma velocidad.

Es más que evidente en este enunciado la presencia de la ley fundamental de las magnitudes, el Principio de Conservación de las Magnitudes según el cual «toda magnitud por si sola permanecerá constante» (no crecerá ni decrecerá).

Es decir, afirma que el único movimiento que se mantiene sin que haya causa alguna es el Movimiento Rectilíneo Uniforme (MRU) y esto no es una afirmación empírica, sino que se adoptada por definición el que cuando un cuerpo se sale de ese tipo de movimiento es porque actúa una «fuerza«, es decir, la aplicación de una «fuerza» desempeña el papel que, con respecto a la conservación de la materia, desempeñaría una entrada de materia desde fuera del sistema considerado.

La Física de Aristóteles es, sencillamente, incompatible con la primera ley del movimiento de Newton, originalmente enunciada por Galileo.

Segunda Ley de Newton

Veamos ahora la «Segunda Ley de Newton» conocida como la «Ley de la Fuerza«. Newton se percató de que había una magnitud constante que resultaba del hecho de que la fuerza aplicada a un cuerpo era directamente proporcional a la aceleración que producía. Y concluyó que esta magnitud debía ser justamente la masa del cuerpo. Esto es, Newton pensó que si a dos masas idénticas (que por lo demás, recuérdese que son constantes, es decir no aumentan ni disminuyen por sí solas) se les aplica la misma fuerza a cada cual por separado y en ambas se producen las mismas variaciones de la velocidad del movimiento, la magnitud que derivará de esa relación debía ser, por consecuencia, constante. En razón de lo cual formuló que:

F = m.a

Quiere decir esto que la fuerza será siempre directamente proporcional a la masa por la aceleración producida. De aquí que formulara el siguiente enunciado:

«el cambio de movimiento de un cuerpo es directamente proporcional al valor de la fuerza que actúa sobre él, efectuándose según la línea recta en dirección de la cual se imprime el movimiento».

El ámbito de enunciación del cual procede este enunciado es el de los saberes matemáticos Por tanto los elementos constitutivos del enunciado serán, en rigor, magnitudes. En este sentido se tendrá que, tanto la fuerza como la masa y la aceleración, constituyen un sistema (una ecuación también suele llamársele) compuesto de tres magnitudes, es decir, un sistema cuyos elementos son puras unidades. De modo que el «texto» del enunciado puede leerse sustituyendo sus elementos estructurales por magnitud. Vale decir: la variación de su conservación (aumento de unidades adicionales), será directamente proporcional a la magnitud que incluyamos en el sistema».

Como dijimos la ley que rige el aumento de una magnitud en un sistema es lo que denominamos la Ley de la Proporcionalidad. Por tanto, es en razón de ella, que en un sistema de tres variables (como fuerza, masa y aceleración) distribuyen sus variaciones de forma proporcional.

Tercera Ley de Newton

Veamos ahora la tercera ley de Newton, conocida como el Principio de Acción y Reacción.

En el despliegue de este discurso de la física clásica, merced a las mismas normas de las modalidades enunciativas del ámbito de enunciación matemática, emergerá otro enunciado conocido como Ley de Acción y Reacción, el cual no será más que otra de las leyes que rigen la existencia de las magnitudes, su comportamiento: distribuciones, reagrupamientos, etc. Me refiero a la mencionada Ley de la Anulación de los Efectos de Variación de las Magnitudes en los Sistemas en Equilibrio:

Como hemos dicho la condición fundante de este discurso de la física moderna es la asunción de lo real como dimensión descualificada, como magnitud, podrá entenderse que la intensidad de la acción de una fuerza no es más que un número determinado de unidades y que el sentido de dicha magnitud (que le da carácter vectorial) no es sino una determinada posición en el conjunto de las magnitudes (recta real): bien a un lado u otro de una magnitud imaginaria que llamamos cero.

De manera que este tercer enunciado newtoniano cierra el campo de enunciación de las magnitudes, y posibilita el despliegue del discurso de la física clásica, en la medida en que postula la tercera ley del movimiento a través de la Ley de Comportamiento de las Magnitudes en un Sistema en Equilibrio: Es con base a esta ley de las magnitudes que Newton sentenció que:

«A cada acción de una fuerza se opone siempre una reacción contraria de igual intensidad, dirigida en sentido contrario».

Con lo cual estaba diciendo que «a toda magnitud, en un sistema que permanezca en equilibrio se le está «oponiendo» (léase mejor, le está acompañando) otra magnitud de igual número de unidades, pero ubicada en lado contrario de la línea imaginaria que marca una magnitud convencionalmente llamada cero». Y con lo cual ha aplicado al mundo físico lo que hemos llamado la «Ley de la Anulación de los Efectos de Variación de las Magnitudes en un Sistema en Equilibrio».

Es con base a este discurso que la física va construyendo los criterios de realidad que signaron a la modernidad por largo tiempo, que marcaron hasta comienzos del siglo XX una forma de ver al mundo: La idea de una masa constante, de un tiempo absoluto, de un universo absoluto, etc. Ya que el universo se tenía como un sistema cerrado: sin entrada ni salida de magnitudes adicionales. Así cada enunciado que va emergiendo en este discurso de la física mecánica debe, de hecho, reafirmar y no contradecir los enunciados fundantes. Es gracias a estas características como el discurso Mecanicista-Newtoniano realizó su despliegue.

Aporia del Movimiento de los planetas y otros cuerpos celestes

En base a estas tres Leyes podemos destacar que la física newtoniana suprime la necesidad de una causa «del movimiento. Queda claro que lo que requiere explicación causal no es el movimiento, es sólo su cambio, es decir, la aceleración.

En efecto, ello responde a que se ha suprimido la diferencia absoluta entre reposo y movimiento, así, de nuevo, aparece la relatividad del movimiento, matemáticamente no existe posibilidad alguna de definir una diferencia entre que un cuerpo A se mueva con respecto a otro B y que sea B el que se mueva con respecto a A, con velocidad de igual valor absoluto y sentido opuesto. Matemáticamente no hay posibilidad de expresar prioridad de un sistema de referencia sobre otro.

Sin embargo, las leyes de Newton solo relativizan la opción entre sistemas de referencia que se muevan el uno con respecto al otro con movimiento rectilíneo uniforme. No obstante, la cosa cambia radicalmente cuando se trata de optar entre sistemas de referencia que se mueven uno con respecto a otro con velocidad variable, es decir, aceleradamente. Por lo que en consecuencia, no son de igual validez todos los sistemas de referencia. Esto constituía toda una aporía para la mecánica newtoniana respecto al Principio de la Relatividad del Movimiento.

Realmente lo que fuerza a Newton son las limitaciones del aparato matemático disponible. El propio concepto newtoniano de «fuerza» está vinculado a la mencionada incapacidad. Limitando así, la validez del Principio de Relatividad del Movimiento. Por ello Newton establece que el espacio es algo «en sí», independiente de los cuerpos y de las relaciones entre ellos, lo que equivale a decir que habría, para Newton, un movimiento «con respecto al puro espacio», esto es, un movimiento absoluto, si bien sería «inobservable». De ahí la necesidad lógica que la física newtoniana experimenta de introducir, para explicar las trayectorias reales y constantes de los cuerpos físicos, una fuerza de carácter universal.

Así el discurso exegético de la física clásica, tenía como criterio de realidad aquel enunciado según el cual «todo movimiento permanece constante a menos que no sea alterado por una fuerza», en razón de lo cual también el movimiento planetario debía regirse por ese comportamiento, para ello se requeriría que la trayectoria descrita por el movimiento de los planetas fuese una línea recta y no una figura elíptica como ya lo había mostrado Johannes Kepler (1571-1630). Luego no podía comprenderse cómo el movimiento de los planetas podía ser elíptico en lugar de rectilíneo.

He aquí que las normas de aparición de los enunciados del discurso de la física clásica operaron haciendo emerger un nuevo enunciado que vino a resolver la aporía, dar sentido de coherencia al discurso; y es en el siglo XVII cuando el discurso físico, de acuerdo a sus propias normas de creación de los conceptos, crea el concepto de «fuerza de atracción entre masas», una fuerza de carácter universal, llamada «gravitación», que vendría a abrir nuevas posibilidades de enunciación.

Ley de Gravitación Universal

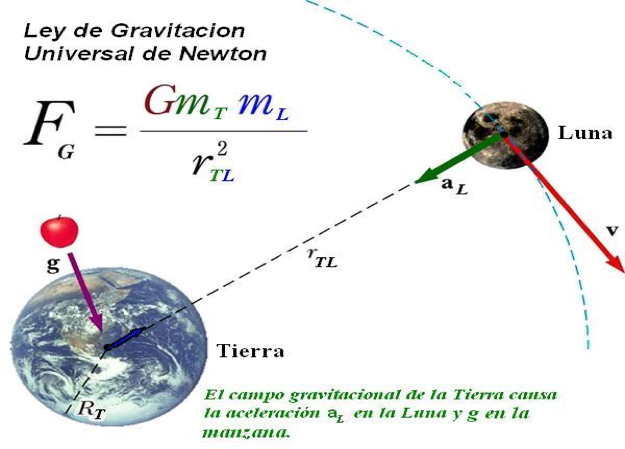
En efecto, Newton en su Principia Mathematica, de 1687 derivó que la única forma de resolver esta aporía era suponiendo que la variación de la «magnitud movimiento» en su dirección y sentido se debía a otra magnitud que él llamó «fuerza de atracción», que «halaba» a los planetas hacia el centro del sol. A este respecto enunció:

«Los cuerpos se atraen con una fuerza directamente proporcional a sus masas respectivas, e inversamente proporcional al cuadrado de la distancia que los separan«. Es decir:

F = G [(m₁. m₂) / r²]

Para salvar la aporía, el nuevo enunciado no sólo respeta la Ley de Conservación de las Magnitudes, sino que además respeta las leyes restantes de comportamiento de las magnitudes en los sistemas, tales como la Ley de Proporcionalidad de la Variación, y la Ley de la Anulación de los Efectos de Variación de las Magnitudes en un Sistema en Equilibrio. Con lo cual los criterios de realidad (masa constante, tiempo constante, etc.) no sólo se mantienen sino que se reafirman. Tal razonamiento supone, también, la existencia de otros sistemas planetarios vecinos, cuyas fuerzas de atracción operan equilibrando a los planetas que se hallen ubicados en las últimas órbitas de los respectivos sistemas.

Epílogo

Así, a partir del siglo XVII la ciencia moderna se pone en marcha, abandonando la jerga de las formas y empleando el lenguaje matemático. Por ello uno de los grandes méritos de los genios más ilustres de esa época fue reconocer esta verdad: la física seguirá leyendo del libro de la naturaleza, pero no será una ciencia clara, precisa, y con consenso universal, hasta que no habla la lengua de las cantidades. Así, ellos crearon lo que hoy conocemos como física, una física matemática, entre ellos el filósofo francés René Descartes (1596-1650):

«No admito en física principios no admitidos también en materia de las cosas corpóreas que aquélla cuya división, figura o movimiento puede ser de cualquier tipo, es decir, la que los geómetras llaman cantidad, y toman por objeto de sus demostraciones; y en esta materia no considero sino sus divisiones, sus figuras y sus movimientos; y en fin, referente a esto, no quiero admitir por verdadero nada que no sea tan evidentemente deducido de aquellas nociones comunes, de cuya verdad no se puede dudar, que pueda ser objeto de una demostración matemática. Y puesto que de este modo se puede dar razón de todos los fenómenos de la naturaleza, como se verá por lo que sigue, no considero que deban ser admitidos otros principios en la física, ni que haya motivo para desear otros que los explicados.» (Descartes, Principia Philosophiae)

«La naturaleza de la materia no consiste en ser una cosa dura, o pesada, o coloreada, o que afecte a nuestros sentidos en cualquier otra forma», sino sola-mente «en ser una sustancia extensa en longitud, anchura y profundidad», (Descartes, Principia Philosophiae) en lo «que los geómetras llaman cantidad» o volumen. De modo que la materia es cantidad.

En esta onda en II Saggitario (1623) escribió Galileo:
«La filosofía está escrita en ese grandísimo libro que continuamente está abierto ante nuestros ojos (a saber, el universo), pero no puede entenderse si antes no se procura entender su lenguaje y conocer los caracteres en que está escrito. Este libro está escrito en lenguaje matemático, y sus caracteres son triángulos, círculos…»

Hemos mostrado que todos los principios fundamentales de la física moderna derivan del postulado de que el lenguaje en el que los fenómenos se expongan ha de ser la matemática. Es a partir de sus enunciados (aún defectuosos, por cierto) cuando el discurso de la física moderna construye los nuevos criterios de realidad y de cientificidad que servirá luego de sustrato para otras ciencias, y para otros saberes que dibujan el horizonte de la modernidad en el ámbito del saber.

Sin embargo, algunas características del sistema newtoniano tales como el espacio absoluto y la gravitación, motivaron muchas críticas de personajes muy influyentes como Gottfried Wilhelm Leibniz (1646-1716).

Sería preciso un ulterior y más profundo desarrollo de la matemática antes de que esta suministrase todos los recursos necesarios para una física concorde con el ideal moderno de la ciencia. Así pues, será con la Teoría General de la Relatividad de Albert Einstein (1879-1955) y su disponibilidad de un nuevo aparato matemático que no solo desaparece toda necesidad de pensar algún sistema de referencia absoluto o «espacio absoluto», sino que desaparece también la distinción entre «inercia» (o sea, conservación del movimiento) y gravitación.

En fin, la formulación y desarrollo de una nueva física fue posible, fundamentalmente, por la posesión de un aparato matemático más potente y, desde luego, por la acumulación de experiencias. Así, la física matemática ha demostrado que era el método físico correcto gracias a los prodigiosos e ince-santes progresos que ha hecho en el estudio de la naturaleza. Por ello hoy en día sería imposible negar, sin chocar con el más elemental sentido común, que las teorías físicas han de exponerse en lenguaje matemático.

Para finalizar debemos recalcar que la mayor de todas las ventajas que se pueden aducir de los conceptos métricos estriba en que ellos constituyen un puente entre el sorprendente y huidizo mundo real y el mundo perfectamente estructurado y ordenado, en fin, Ideal, de la matemática. Sin embargo, resulta sorprendente que ese rodeo por el mundo ficticio de la matemática nos proporcione representaciones fiables del mundo real de los procesos físicos y soluciones eficaces a nuestros problemas empíricos. Parece milagroso que algo tan extravagante funcione.

Al respecto, el físico inglés Paul Davies (1946-) nos dice: «Quizá el mayor descubrimiento de todos los tiempos es el de que la naturaleza está escrita en código matemático»… También el físico húngaro Eugene Wigner (1902-1995) expresó: «El milagro de la adecuación del lenguaje de la matemática para la formulación de las leyes de la física es un don maravilloso que nosotros no entendemos ni merecemos». Quizá no lo merezcamos, pero sí, a pesar de todo, tratamos de entenderlo, tendremos que seguir avanzando en nuestra comprensión de la estructura, dinámica y papel de los conceptos métricos en la empresa científica. Lo cierto es que son parte de nuestros «Criterios de Realidad» del siglo XXI, nuestras «Verdades Vigentes».
Venga, ¡La Ciencia no ha llegado al final, nos queda un largo camino por aprender acerca de cómo funciona la naturaleza!