¿Saben cuál es el número más grande que es «útil» para las matemáticas?
Pues es… el Número G de Graham
En las próximas líneas voy a tratar de aproximarles a él. Venga, para que tengan una mínima idea de cuán grande es, pero casi podría asegurar que no lo entenderán, es que ni ustedes, ni nadie, literalmente puede hacerlo, es inconcebible, es inimaginable…
Para ubicarles en su historia les diré que recibe su nombre de Ronald Graham, profesor del Departamento de Ciencias de la Computación de la Universidad de California, en San Diego. Ahhh, y el tal Graham no es un matemático común… Noo. Es un matemático fanático del malabarismo y del trampolín, que incluso ha actuado en el Cirque du Soleil… ¡Vaya personaje!

Realmente hay números muy grandes, por ejemplo, si nos propusiéramos contar a ver hasta dónde llegamos y contáramos una cifra por segundo las 24 horas del día, para contar hasta 1000 tardaríamos 17 minutos. A un millón 12 días, mil millones 32 años y un billón, 32.000 años, que es un tiempo superior al de la existencia de la civilización en la Tierra.
 Pero vayamos a los realmente grandes. Comenzaré diciéndote que el Número de Graham es mucho mayor que otros conocidos números increíblemente grandes tales como el googol (Venga, un googol es 10100), o el un googolplex (Un googolplex es 10googol).
Pero vayamos a los realmente grandes. Comenzaré diciéndote que el Número de Graham es mucho mayor que otros conocidos números increíblemente grandes tales como el googol (Venga, un googol es 10100), o el un googolplex (Un googolplex es 10googol).
Es que el Número de Graham es tan ridículamente enorme que el googolplex sería tan chiquitico como sería el primer paso de un paseo a pie desde acá hasta más allá de la galaxia más lejana que podamos imaginar.
¿Por qué es importante ese descomunal número? Resulta que es el mayor número jamás usado en una demostración matemática. En efecto, es un gran número que es cota superior de la solución de un determinado problema en la rama de las matemáticas conocida como la Teoría de Ramsey:
Considérese un hipercubo n-dimensional, y conéctese cada par de vértices para obtener un grafo completo con 2n vértices. Posteriormente, coloréese cada una de las aristas de negro o de rojo. ¿Cuál es el menor valor de n para el cual toda manera de colorear las aristas necesariamente da lugar a un subgrafo completo de un solo color con 4 vértices que forman un plano?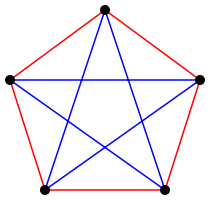
La resolución de este problema no es nada sencilla, y además su solución no es un número definido… es un número acotado, es decir, que se sabe, con toda seguridad, que tiene que estar entre dos ciertos valores. Basta decir que Graham y Rothschild en 1971 demostraron que este problema tiene una solución, N*, y dieron como acotación de la misma 6 ≤ N* ≤ N, siendo N un número determinado, definido explícitamente y muy grande. Ronald Graham consiguió esta cota superior, y luego fue Martin Gardner en la sección «Mathematical Games» de la prestigiosa revista Scientific American de noviembre de 1977, quien lo apodó como el “Número de Graham”.
Debo comentar que la cota inferior fue posteriormente mejorada por Exoo en el 2003, quien mostró que la solución es al menos 11 y proporcionó evidencia experimental que sugería que era al menos 12. Con esto, la estimación más conocida para la solución N*, del problema que mencioné, es 11 ≤ N* ≤ G, donde G es el Número G de Graham.
El número de Graham y la flecha de Knuth
Como les dije, el Número de Graham es tan, pero tan, grande que de hecho, es difícil tratar de fijar una idea o pensamiento sobre él, está fuera de nuestra percepción… Es que es imposible, dadas las limitaciones de espacio y materia de nuestro universo, denotar el Número de Graham, o una aproximación razonable del mismo, en un sistema de numeración convencional… En efecto, no sirve ningún sistema de numeración para expresar este número, ni el Sistema Decimal, ni las potencias, ni las torres de potencias, nos podíamos pasar toda la vida elevando potencias a otra potencia a otra potencia y no llegaríamos nunca a acercarnos al Número de Graham. Pero si hay una forma de describirlo, y así lo hizo Graham, es utilizando fórmulas recursivas por medio de la notación flecha de Knuth.
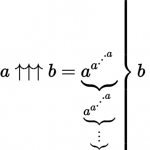
En efecto la notación sagital de Knuth es muy especial, utiliza operadores flechas, y nos permite desarrollar un método que nos llevará al Número de Graham.
Veamos, con ejemplos, cómo trabaja. Comencemos con un solo operador flecha:
3↑2 = 32 = 9 (Así, el número que está a la izquierda de la flecha nos indica la base y el número que queda a la derecha es el exponente de nuestras conocida potenciación, en inglés “Exponentiation”).
La tetración es la exponenciación iterada. Por ejemplo 6 tetrateado por cuatro significa cuatro seis elevados el uno al otro: 6666(Ojo, contando el 6 de la base).
Veamos cómo trabaja dicha tetración utilizando ahora dos operadores flechas. En este caso el número que está a la izquierda de la flecha nos indica la base y es el número con que construiré la torre de potencias, y el número que queda a la derecha es el número que define la altura de la torre de potencias, es decir la cantidad de exponentes, incluyendo la base primera, que figuran en tal torre de potencias.
3 tetrateado por tres, será:
3↑↑3 = 333 = 327 = 7.625.597.484.987
Debo resaltar que la operación de tetración con ésta Notación de 333 es 327 y el resultado es 7.625.597.484.987 y no 39 = 19.683 como, tal vez, podrías creer.
Vayan notando el crecimiento. Sólo con una pequeña torre de potencias construida a base de 3s (sólo utilicé 3 de ellos) y el resultado ya nos da más de 7.6 billones.
El paso siguiente sería añadir un tercer operador flecha:
3↑↑↑3 (tres pentateado por tres) redefine una nueva torre de potencias construida de 3ses donde el número de tres (de exponentes en nuestra torre de potencias) queda definido por la cantidad anterior es decir, serán 7.625.597.484.987 tres, uno encima de otro… y aunque 7.6 billones es un número grande, podemos considerarlo todavía pequeño (venga, lo podemos todavía expresar fácilmente con dígitos) pero el resultado de la operación (3 elevado a la 3, elevado a la 3, elevado a la 3, elevado a la 3…y así sucesivamente, 7.6 billones de veces) será un número absurdamente grande, y ni idea cuál sería el resultado para escribirlo en nuestra forma decimal.
Vamos ahora a un paso crucial… agreguemos un cuarto operador flecha:
3↑↑↑↑3 (tres sextateado por tres) esto redefine una nueva torre de potencias construida de 3ses donde el número de tres (de exponentes en nuestra torre de potencias) queda definido por la el resultado de la cantidad anterior. Es decir, serían 3↑↑↑3 tres, uno encima de otro… Una monstruosidad de torre matemática que ni idea tenemos cuál sería su tamaño. Ahhh, y el resultado final sería un número que no sólo es absurdamente grande e inconcebible, sino que además, es infinitamente mayor que el anterior.
El procedimiento continuaría en forma análoga cada vez que se agregue un operador flecha más a la expresión anterior es decir, el número de tres (de exponentes en nuestra torre de potencias) será el resultado de la operación anterior. Pienso que ahora será entendible como aumentan exorbitantemente los resultados de la operación con sólo añadir un operador flecha más a la cantidad anterior.
No obstante, si escribimos operadores flechas uno después de otro, entre 3ses, en todo momento del tiempo de nuestras vidas… la cantidad resultante de tal operación es irrisoria con respecto a la cantidad que buscamos… el Número de Graham.
Como insinué, para expresar el “Número de Graham” todo lo que puede hacerse es desarrollar una serie numérica, una sucesión. Eso fue lo que hizo Ronald Graham, veamos su desarrollo:
Comenzamos la serie con el término inicial g0 = 3↑↑↑↑3
Claro que este número no es el Número de Graham. Este número se llama g0. La magnitud de este primer término, g0, es tan grande que está realmente más allá del ámbito de la comprensión humana.
Ahora cabe subrayar que, después de este término, quedan muchos más términos en esta sucesión rápidamente creciente, antes de llegar al Número de Graham.
El segundo término de la serie es g1 = 3↑↑↑↑… “g0 Operadores flechas”…↑↑↑↑3
Es decir, para g1 habrá g0 número de flechas entre 3ses, es decir g1 = 3↑↑↑↑……↑↑↑↑3, donde el número de ↑ es el resultado de g0, en este caso estamos tomando un número de pasos que es un número increíblemente grande. Y cuando hayamos terminado, tendremos de resultado un número al que llamaremos g1… Ni siquiera empiece a pensar en lo grande que es g1. En realidad es imposible.
Seguimos adelante. Como seguro ya usted vaticina, ahora simplemente se hace una operación de orden g1 en dos tres, y lo llamamos g2.
El tercer término de la serie es g2 = 3↑↑↑↑… “g1 Operadores flechas”…↑↑↑↑3
Y de forma análoga tendremos que:
El cuarto término de la serie será g3 = 3↑↑↑↑… “g2 Operadores flechas”….↑↑↑↑3
Debemos poner atención que no es, como explicábamos anteriormente, aumentar de uno en uno los Operadores Flechas… Es aumentar el número de operadores flechas en base al número del resultado anterior de la serie, lo cual es infinitamente más grande, de paso a paso, que lo que habíamos explicado anteriormente…
De esta forma vamos avanzando término a término según esa regla, o norma matemática, de formación y cuando lleguemos al término 64 (g64) habremos llegado… al Número de Graham (G).
Ahora debería ser entendible el por qué dijimos que era perturbador, inconcebible inabarcable a la mente humana. Es que no hay nada en el Universo imaginable e inimaginable que se pueda hacer corresponder con semejante cantidad. Hasta el lenguaje se nos presenta inútil para hablar de estas cantidades.
Una forma de escribir de una forma más elegante el Número de Graham sería así:
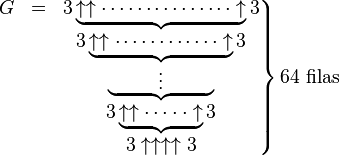
Donde, como dije, el número de flechas en cada fila, empezando por la fila superior, viene especificado por el valor de la fila inmediatamente inferior, es decir:
G = g64 donde g0 = 3↑↑↑↑3 = 3 ↑4 3 y gn= 3↑gn-1 3
Y luego seguimos adelante, y así sucesivamente, hasta g64, que es el propio Número G de Graham.
Recapitulando lo aprendido
G se calcula a través de 64 pasos: el primer paso consiste en calcular g0 con cuatro flechas entre los 3ses; el segundo paso consiste en calcular g1 con g0 flechas entre los 3ses, el tercer paso consiste en calcular g2 con g1 flechas entre los 3ses, y así sucesivamente hasta calcular finalmente G = g64, que tiene g63 flechas entre los 3ses.
No es una sorpresa decir que este es un número increíblemente enorme, tan grande que si pudiéramos escribir cada número del número de Graham en cada átomo del universo observable, no sería suficiente. Como resultado nunca aprenderemos cuántos dígitos tiene, el número es demasiado grande para ser almacenado en la precisión por cualquier computadora que haya existido o existirá nunca. Y, ¿por qué se puede afirmar esto? Porque incluso escrito en notación científica, el número de dígitos en el exponente excedería el número de átomos en el universo observable.

Muy interesante su artículo, profesor Edgar Redondo. Siento que es un área filosóficamente atractiva, donde entra en juego el Número de Graham.
Definitivamente el desorden completo es imposible.