Reflexiones sobre el Número de Graham

Lee el artículo anterior sobre el Número de Graham

Es realmente fascinante el Número G de Graham. Comenzamos con números que en demasía son muy grandes para encajar en nuestra realidad, y luego los elevamos a potencias más allá de la comprensión de nuestros cerebros.

Verdaderamente, el Número G de Graham es, sin exageración, demasiado grande para encajar en nuestra realidad, literalmente no se puedo ni imaginarlo y no son habladurías. De hecho, si como dicen demostrado los números son información, y la información tiene una relación fundamental con la entropía, y la entropía con la energía, y la energía con la masa. Todo eso significa que no hay manera, ni siquiera con la Física Cuántica de conocer explícitamente ese número.

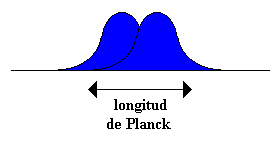
En efecto, recordemos la famosa Longitud de Planck, venga, el menor espacio medible que existe, algo así como el tamaño de “Resolución” de la realidad. Es que la longitud de Planck (ℓ_P =1.616 229 ×10 ^-35 metros) es la distancia límite por debajo de la cual las mismas nociones de espacio y longitud dejan de existir, teóricamente se considera por los teóricos de la gravedad cuántica que es la cuantificación del espacio que constituye el tejido del Universo, también conocida como “Espuma Cuántica”. Así, los radios del quark up, el quark de encanto (charm quark) y el quark superior (top quark) son alrededor de 10^-18, 10^-19 y 10^-22 metros, respectivamente.

No debemos olvidar que las mediciones astronómicas indican que la Tierra es una insignificante mota de polvo cósmico en un Universo observable con un más que inimaginable tamaño de 93.000 millones de años luz de diámetro. Sin embargo, estas más que mareantes cifras pueden que no sean más que una otra insignificancia más, porque si la Teoría de la Inflación Cósmica es correcta, resultaría que el Universo más allá de nuestra observación sería ¡150 mil trillones de veces más grande que el observable!…y de esas cositas es de lo que estamos hablando.

Pues necesitamos alrededor de 100.000.000.000.000 (10¹⁴) de longitudes de Plack ℓ_P para cruzar el diámetro aproximado de un quark. Ahora imagine que cada espacio cúbico de Longitud de Planck pudiera usarse para almacenar un dígito binario. Un quark tendría 10 elevado alrededor de 3000 ceros de ellas, suficiente para almacenar información sobre cada átomo en el sistema solar. Pero no necesitamos un quark. Si almacenamos un bit en cada longitud de Planck cúbica en el Universo conocido todavía no tendríamos suficiente espacio para almacenar el Número G de Graham, Incluso ni siquiera alcanzaría para albergar a g₀. El resultado de este primer paso de la iteración es fácilmente mayor que el número de volúmenes de Planck en los que el Universo observable puede ser dividido. Si todo el Universo observable fuera una computadora, y cada pequeño quark y neutrino representara un bit de data, como dije no podía almacenar tal número entero con precisión.

Es increíble pero el cálculo completo de g₀ literalmente destruiría el universo. No es una exageración llevada a niveles del Microcosmos. Son escalas repetidas en términos que nadie puede imaginar. Ahhh y todo a nivel de g₀, el término inicial de la serie, venga, antes de que realmente hayamos comenzado a subir. Todo indica que tenemos un número que el Universo en sí mismo no podría representar.

Es bueno aclarar que, por supuesto, el Número G de Graham es inimaginablemente grande, y por ello apareció en el Libro Guinness de los Récords. Pero, no es el número más grande que podríamos tener o imaginar, bastaría sumarle uno y ya tendríamos uno más grande, o multiplicarlo por 2 y tendríamos uno el doble de grande, y ni pensar en el g₆₅ o en el g_{NumeroDeGraham}, ese, ese si sería mucho más grande.

En fin, producto de la situación antes planteada, la realidad del Número G de Graham da para innumerables cavilaciones.

Reflexiones Epistemológicas en relación al Número de Graham

Otra semilla de reflexión, que nace con el Número G de Graham, cae dentro del terreno de la Epistemología, al poner G en tela de juicio a todo un conjunto de conceptos y categorías. Así, muy posiblemente, por hechos como éste, será necesario refundar nuevos constructos que funden nuevas racionalidades y nos permitan llegar a una nueva Filosofía de la Ciencia.

Permítanme indagar un poco, partiré del hecho de que las cosas son explicables y descriptibles sólo con relación a un Sistema, y el Sistema más profundo, desde donde se puede comenzar a esbozar «verdades» es, precisamente, el Sistema Epistemológico que fundamenta toda investigación científica principalmente a través, primero de la Dimensión Gnoseológica que explora las vías de su producción y/o validación, y segundo, a través de la Dimensión Ontológica, donde se desarrollan ciertos cuerpos de convicciones acerca de la naturaleza del conocimiento.

Desde la Gnoseología, parece evidente que el origen del conocimiento, es decir, el proceso en virtud del cual la realidad se refleja y se reproduce en el pensamiento humano, en la investigación que da origen al Número G de Graham, se encuadra con el Racionalismo, donde destaca que la manera de conocer es el razonamiento.

Otro acto Epistemológico Gnoseológico es el referido a la posición en lo referente a la posibilidad del conocimiento, acá aflora el Dogmatismo que plantea el que somos capaces de alcanzar verdades estables, independientemente de las épocas y los espacios, de las creencias y las opiniones.

En cuanto al Fundamento Ontológico que define nuestra concepción sobre la “Realidad” y el “Ser” de las cosas, es decir, al « ¿Qué hay?», al estudio de las “esencias”, a las posibilidades de las “existencias”, cabría preguntarse si ¿Podemos darle título de existencia a una realidad que no puede existir en nuestro Universo? Si la respuesta es sí, la Concepción Ontológica de la investigación que dio origen al Número G de Graham es menos evidente que se enmarque dentro del Realismo, es decir aquella concepción que cree que hay una “Realidad” real, externa a la propia conciencia, así como que la naturaleza es siempre cognoscible, aunque nuestras capacidades de examinar esa “Realidad” sean completamente limitadas, el sujeto construye el conocimiento de esa “Realidad”, aunque en el caso del Número G de Graham tendríamos que ampliar esa visión ya que en este caso es indiscutible que el conocimiento amplia la “Realidad” conocida, hasta más allá del Universo.

A pesar de las interesantes variantes que se generan, podemos afirmar que la investigación que generó el Número G de Graham con ciertos cambios encuadra, dentro de la Epistemología, con el “Enfoque Racional Deductivista”, que tradicionalmente se basa: Gnoseológicamente en el Racionalismo, así como en el Escepticismo, pero, en este caso, encaja dentro del Dogmatismo y Ontológicamente basada en el Realismo, pero un “Realismo” sin espacio-tiempo en nuestro Universo.

A raíz de situaciones como esta, cabría preguntarse sí ¿Prevalecerán en el futuro los viejos conceptos Epistemológicos para toda la fundamentación filosófica de la Ciencia?

Como con la investigación que dio origen al Número G de Graham, ya comienzan a parecer evidencias de que no va a poder ser. Sí la Filosofía aspira a seguir desempeñando un papel importante en los momentos que nos comienzan a brindar las nuevas “Realidades”, es preciso que se alimente con los avances actuales en la Ciencia.

Reflexiones dentro de la Lingüística sobre el Número de Graham

Otras reflexiones sobre el Número G de Graham y su “Realidad” tampoco caen dentro del terreno matemático, por ejemplo un terreno muy fértil sería la Lingüística. La tesis fundamental del Tractatus logico-philosophicus, de Ludwig Wittgenstein, es la estrecha vinculación entre lenguaje y mundo, hasta tal punto que: «los límites de mi lenguaje son los límites de mi mundo» es decir, hay una relación isomórfica entre lenguaje y mundo, la realidad es aquello que se puede describir con el lenguaje y así tenemos que el lenguaje humano es el mayor factor limitante del pensamiento y de la comunicación humana. Sin embargo, todo parece indicar que el pensamiento humano no puede seguir el ritmo de su propia visión, vemos, con el Número G de Graham, que el poder de las palabras se agota, más sin embargo, podemos escribirlo, utilizando una fórmula recursiva, en un pequeño trozo de papel en mucho menos de un minuto en el lenguaje de las matemáticas.

Reflexiones dentro de la Filosofía Matemática

Finalmente, otra semilla para la reflexión cae dentro del campo de la Filosofía o fundamentación de la Matemática. Es sabido que en la Filosofía de la Matemática, el Platonismo y el Constructivismo se presentan como una dualidad disyuntiva, ya que ambas se oponen a diversos grados. Analicemos un tanto esta situación para que aflore, a través del Número G de Graham el por qué no la compartimos.

El Platonismo, en Filosofía de la Matemática, postula que detrás del mundo físico, sensible y dotado de movimiento, existe un mundo objetivo, habitado por ideas o universales abstractos, inmutables y omnitemporales que pueden combinarse para formar verdades o falsedades exactas y definitivas, que podemos a veces descubrir. Un mundo perfecto, sobre el cual no podemos tener ninguna influencia. En el proceso de descubrimiento, el lenguaje tiene un rol secundario y accesorio. Según el Platonismo, los objetos matemáticos ya existen y mantienen ciertas relaciones entre sí, independientemente de nosotros; y lo que hacemos es descubrir estos objetos y las relaciones que se dan entre ellos.

Quiero aclarar que para el Idealismo, muy al contrario, el mundo objetivo independiente de nuestros símbolos es un sueño. El Universo está en el símbolo. No hay verdad matemática en sentido Ontológico; toda verdad es Epistemológica y depende de nuestra percepción, de nuestra expresión, de nuestro lenguaje que no es solamente el traje con que se viste la verdad sino su contenido mismo.

Ahora bien, normalmente el constructivista opone a esto la imagen de que nosotros elaboramos -construimos- las entidades matemáticas conforme las desarrollamos.

En efecto, el constructivista exige una regla o un cálculo que le permita demostrar, producir o reconocer la existencia de un objeto o de una propiedad cuya existencia es presupuesta, o afirmada, explícitamente por un teorema. Se necesita un algoritmo, es decir, un proceso enteramente planificado, y por ende finito, que opere sobre configuraciones finitas, en etapas discretas y simples, donde cada paso esté determinado por el paso que le precede. Una prueba es constructiva si cada vez que implica la existencia de algo se muestran los procedimientos que permiten su construcción. El constructivista inventa o construye las verdades matemáticas, no las descubre: la prueba crea la existencia.

Así mismo, para Wittgenstein ningún descubrimiento matemático puede tener influencia alguna en la Filosofía de la Matemática, con lo cual no estoy nada de acuerdo. Parece que tuviéramos que intercalar entre la imagen platónica y la constructivista una imagen intermedia, y así romper con la dicotomía entre las imágenes platónicas y constructivistas que se ventilan en la Filosofía de la Matemáticas, por ejemplo, en nuestro caso del Número G de Graham, la de objetos que aparecen repentinamente en respuesta a una investigación. Acá no se construye el objeto, sino que se aceptan conforme los encontramos, pero no es que estuvieran allí antes de llevar a cabo las investigaciones que los traen al «Ser».