El Número de Euler o La Constante de Napier

Aunque no lo creas…La siguiente es una regla mnemotécnica para recordar el número “e”:

«El trabajo y esfuerzo de recordar e revuelve mi estómago, pero podré acordarme. Será fácil si leo todas las frases. La repetida canción será cantada y así verás el número huevón”.

En ella el número de letras de cada palabra representa la secuencia ordenada de las primeras 33 cifras y cada punto representa un cero.

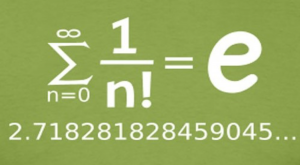
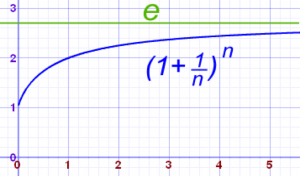
Así como pi  es fundamental en la Geometría y el número “i” en el  Análisis Complejo y el Álgebra. “e” es la base de los logaritmos naturales y formar parte de las ecuaciones del interés compuesto, juega un papel importante enel Cálculo, y en el Análisis en la definición de una de las funciones más importantes de la matemática: la función exponencial e^x, un instrumento usado de una u otra forma, para describir el comportamiento del crecimiento de las cosas (reacciones químicas, físicas, eléctricas, celulares …). Es la única función de x con una tasa de cambio con respecto a x igual a la función misma. En otras palabras, cuando un fenómeno se comporta de manera exponencial, tiene la propiedad de que su ritmo de cambio es proporcional al ritmo de cambio de su variable. Ello explica el que la derivada de la función e^x sea la misma función.

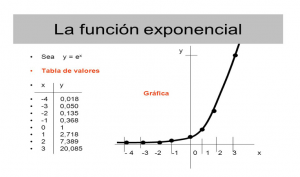
Realmente pi   siempre se lleva toda la atención del público, pero la verdad es que “e”, que también es irracional (no expresable mediante una razón de dos números enteros), es súper-cool.

José Acevedo Jiménez le escribió un poema que quisiera compartir con ustedes:

Singular y encantador es el número (e).
Sus primeros nueve dígitos decimales no deben confundirte,
718281828, el 18 28 que se repite, pues al igual que (pi) es un número
irracional.
De la fórmula del interés compuesto, extiende el límite hasta el infinito y
comprenderás lo que digo.
¡Oh! qué número tan fascinante que aparece en las finanzas, del cálculo de
Newton y Leibniz ni hablar, que ha encontrado en los logaritmos de

Neper su
morada al ser su base natural.
Intrigante es el número (e), que al elevarlo a la su derivada permanece

igual;
¡qué grandioso trascendental! sin ser su intención del gran Euler es la

inicial y en
las funciones trigonométricas hiperbólicas lo podemos encontrar, a ese
interminable numeral.
Las estrellas lograremos contar, más las cifras de (e) jamás, pues como

cociente de
enteros nunca lo podremos expresar; y como por mandato divino,
con (pi) y la
unidad imaginaria se puede relacionar mediante una hermosa identidad,
que sólo a Euler se le pudo revelar. Por eso y mucho más en diversas

ramas de las
matemáticas el número (e) nunca, jamás
ha de faltar.

José Acevedo Jiménez

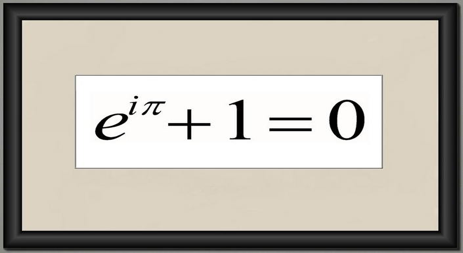
Pero bueno, entremos en materia… Vamos a lo sorprendente… Para ello vamos hacer  un experimento mental…

Elige un número aleatorio entre 0 y 1 y anota su valor.

Haz esto de nuevo y suma el segundo número al primer número.

Sigue  haciendo esto hasta que la suma de los números aleatorios supere, o rebase, a 1.

¿Cuál es el valor esperado (o media) del número de números aleatorios necesarios para lograr esto?

Pues, sorpresa…  Es e (2.718281828459045…) el número promedio de números aleatorios entre 0 y 1 que deben ser sumados para que su suma de al menos 1. Es decir, si tuvieras que tomar y sumar números aleatorios entre 0 y 1, en promedio, necesitarías e (2.718 …) números, para llegar a por lo menos 1.

Les dejo un Link de una corrida de ejemplo:

https://jsfiddle.net/NathanFriend/339nyLm6/